Hola!
Tras una semana con el acertijo a la espera de vuestras soluciones, llega la hora de desvelar las respuestas correctas y cómo las hemos conseguido nosotros. En esta ocasión os contábamos que todos los números tienen una única descomposición en factores primos, pero que recolocando los factores el número de formas de escribir cada descomposición varía. Por ejemplo:
12 = 2 × 2 × 3 = 2 × 3 × 2 = 3 × 2 × 2
lo que indica que la descomposición de 6 se puede escribir de 2 formas, y la de 12 de 3. Os preguntábamos por los números más pequeños cuya descomposición en factores primos puede escribirse, exactamente, de 6, 10 y 45 formas. En los comentarios, Ferrán nos dio su solución para 10 y 45 formas y ¡era correcta! incluso aunque nuestro planteamiento del acertijo no era del todo claro y tenía dudas. Os retamos con una pregunta más, 72 formas, y Gualterio la contestó también correctamente. ¡Enhorabuena a ambos! Curiosamente, nadie contestó a la primera pregunta, la de 6 formas…
Veamos cómo resolvimos nosotros el acertijo. Si vuestra solución es diferente, ¡no dudéis en contárnosla!
El primer paso es analizar por qué la descomposición en factores primos del 6 se puede escribir de 2 formas y, después, por qué la de 12 se puede escribir de 3. Para eso, nos apoyamos en la rama de las matemáticas denominada combinatoria que ya ha aparecido en algún otro acertijo. En el caso que nos ocupa, si miramos la descomposición del número 6 vemos que tenemos dos números primos distintos (el 2 y el 3) y queremos saber de cuántas formas diferentes podemos colocarlos. Dicho de otro modo, ¿de cuántas formas puedo colocar n elementos? Esa pregunta la responden las permutaciones. No es muy difícil llegar a la fórmula matemática de… n! o, «factorial de n» que es la multiplicación de todos los números entre 1 y n.
El caso del 12 es más complicado, porque hay factores repetidos. Debido a ello, el concepto de permutación no nos sirve directamente, y hay que complicarlo un poco más con las permutaciones con repetición. De nuevo, volviendo a las matemáticas, si tenemos n elementos, donde hay a iguales entre sí, otros b iguales entre sí, etcétera (con todos ellos sumando n) entonces el número de formas de colocarlos (o sea, las permutaciones con repetición) son:
Con esto, analizamos lo que ocurre con el número 12. Su descomposición en factores primos tiene tres números (2 × 2 × 3), por lo que n es 3. Además, hay dos que se repiten, por lo que a=2 y b=1. Por tanto:
Esto significa que las matemáticas nos dicen que la descomposición de 12 la podemos poner de 3 formas diferentes, tal y como vimos escribiendo a mano todas las opciones.
Vamos ahora con las preguntas. La primera era ¿cuál es el número más pequeño cuya descomposición en factores primos se puede escribir de 6 formas? Es decir, estamos buscando los valores de n, a, b, … tales que:
Esto no tiene una solución sencilla, por lo que nos dedicaremos a tantear. Pero en lugar de ponernos a hacerlo ciegamente, empezaremos descomponiendo en factores primos el número 6, para que su «radiografía» nos dé una pista de con qué números empezar a probar. En concreto, sabemos que 6 = 2 × 3.
Además, nos vamos a apoyar en la descomposición en factores de los factoriales. Por ejemplo:
3! = 3 × 2
4! = 4 × 3 × 2 = 23 × 3
4! = 5 × 4 × 3 × 2 = 23 × 3 × 5
…
Si lo hacemos con más números, terminaremos sacando la siguiente tabla, donde mostramos el número de veces que aparece cada número primo en los factores de cada factorial (hasta 10):
| 2 | 3 | 5 | 7 | |
|---|---|---|---|---|
| 2! | 1 | |||
| 3! | 1 | 1 | ||
| 4! | 3 | 1 | ||
| 5! | 3 | 1 | 1 | |
| 6! | 4 | 2 | 1 | |
| 7! | 4 | 2 | 1 | 1 |
| 8! | 7 | 2 | 1 | 1 |
| 9! | 7 | 4 | 1 | 1 |
| 10! | 8 | 4 | 2 | 1 |
La tabla indica que, por ejemplo, 6! = 24 × 32 × 51
Mirando esta tabla y lo que queremos conseguir:
es fácil llegar a la conclusión de que:
De aquí, podemos deducir que el número más pequeño cuya descomposición tiene 6 formas de escribirse tiene tres factores diferentes (por los tres unos en el denominador). Para que el número sea lo más pequeño posible, cogemos los factores (primos) más pequeños posibles y por tanto la respuesta es:
La segunda pregunta era el número más pequeño cuya descomposición se puede escribir de 10 formas. Sabemos que:
y queremos escribirlo de la forma:
Éste es un poco más complicado, de modo que vamos más despacio. Para el n! del numerador necesitamos encontrar un factorial que incluya en su descomposición un 2 y un 5. Para eso, recurrimos a nuestra tabla y vemos que 5! es 23 × 3 × 5. Por comodidad, representaremos sólo los exponentes, por lo que diremos que 5! es (3, 1, 1). Por su parte, 10 lo representaremos como (1, 0, 1) pues su descomposición es 21×30×51.
Fijaos que en este caso el factorial de 5 incluye más factores que 10, y hay que «quitarlos» dividiendo por a!, b!, etcétera. En concreto, si «restamos» la representación del 5! (3, 1, 1) y del 10 (1, 0, 1) nos queda (2, 1). Tenemos que conseguir esa descomposición usando factoriales para ponerlos en el denominador. Mirando en la tabla, es fácil ver que eso se consigue con 3! y con 2! de modo que ¡ya lo tenemos!:
Es importante asegurarse de que los números del denominador suman lo mismo que el numerador, es decir que n = a + b + …. En este caso esto se cumple. Lo único que falta es sacar el número de la respuesta. Cualquier número que tenga dos factores primos diferentes, uno elevado al cubo (por el 3!) y otro al cuadrado (por el 2!) tendrá exactamente 10 formas de escribir su descomposición. Como queremos el más pequeño, usamos los primos más bajos, y eso nos da:
tal y como nos dijo Ferrán en los comentarios 🙂
Vamos con el último, el 45 = 3 × 3 × 5. Igual que antes, ésto lo representamos como (0, 2, 1). Fíjate que empezamos con un 0 porque el 2 (el primer número primo) no aparece en la descomposición. Ahora necesitamos buscar en nuestra tabla de la descomposición de factoriales el primero que incluya dos treses y un cinco. Ese resulta ser 6! (4, 2 1). Ahora necesitamos buscar una forma de «quitar» los cuatro doses y para eso la única opción es poner en el denominador cuatro 2!:
Pero… ¡¡cuidado!! Esta solución no sirve, porque la suma de los denominadores (2+2+2+2) es mayor que el numerador (6) y por tanto no es una fórmula válida para las permutaciones sin repetición. Por tanto hay que probar con un número mayor en el numerador. El problema es que al subir a 7! nos aparece un primo más en la lista que tendremos que quitar, dejando de todos modos los dos treses y el cinco de la descomposición del 45. Analizando la tabla y haciendo pruebas mentalmente, veréis que la única opción válida es:
El número que estamos buscando, por tanto, es 28 × 32 que es 2304, como también nos dijo Ferrán.
Si utilizáis la misma técnica, veréis que la última pregunta que os hacíamos en los comentarios, 72, tiene como respuesta 1920, tal y como nos dijo Gualterio.
Tened en cuenta que nos hemos tomado algunas licencias con las respuestas, porque las preguntas que os hicimos estaban escogidas con cuidado. En realidad en ocasiones no es suficiente con encontrar la primera forma de escribir el número original, sino que es necesario seguir subiendo. Por ejemplo:
Por tanto, cualquier número con 6 factores diferentes tendrá 720 formas de escribir su descomposición, y, al mismo tiempo, cualquier número con 10 factores de los cuales 7 son el mismo (y los demás son distintos) también. Resulta que con la primera configuración (6 diferentes) el número más pequeño es el 30.030, pero con la segunda (10 factores, 7 de ellos iguales) es el 13.440, que es más pequeño y por tanto preferible. En ninguna de nuestras preguntas ocurre eso (aunque todos se pueden escribir de más formas usando numeradores mayores). No obstante, que pueda ocurrir hace más difícil programar una solución. Pero si te atreves, siempre podrás probarla aquí 🙂
Este ha quedado muy matemático… en el próximo intentaremos compensarlo 🙂
Chao!
¡Hola!
Vamos con un nuevo acertijo. Esta vez nos vamos a atrever con un acertijo un poquito más complicado que los demás, porque requiere dar varios «pasos mentales» para llegar a la forma de resolverlo. Además, en contra de lo que suele ocurrir, conseguir la solución con la ayuda de un ordenador resulta ser más difícil que hacerlo a mano… de modo que cerrar vuestro editor de código favorito, coged un lápiz y un papel y… ¡manos a la obra!
El planteamiento del acertijo es bastante simple. Es bien sabido que cualquier entero positivo se puede representar de forma única como una multiplicación de números primos. Aunque no es importante para nuestro acertijo, es lo que los matemáticos llaman el teorema fundamental de la aritmética.
Por ejemplo:
12 = 2 × 2 × 3
Aunque, efectivamente, esta descomposición en factores primos es única, en realidad la mayoría de las veces puede escribirse de más de una forma. Por ejemplo:
12 = 2 × 2 × 3 = 2 × 3 × 2 = 3 × 2 × 2
Vemos que la descomposición del 6 puede escribirse de dos formas, y la del 12 de 3. Además, no hay ningún número menor que 6 cuya descomposición se pueda escribir de 2 formas, ni ninguno menor que 12 que se pueda escribir de 3.
¿Cuál es el número más pequeño cuya descomposición en factores primos puede escribirse de 6 formas? ¿Y de 10? Y… ya que nos ponemos… ¿de 45?
Como siempre, si das con la solución y la programas, puedes probarla aquí. Aunque te recordamos que, en esta ocasión, es más fácil resolverlo a mano (después de pensar un rato) que con un ordenador 🙂
¡Hasta el domingo!
Hola!
Vamos, un domingo más, con la respuesta del acertijo de la semana. En él, os hablábamos de una carretera que cruza el territorio del lince ibérico, en peligro de extinción. Para evitar atropellos, se pusieron vallas en varios tramos. Sin embargo, los linces seguían cruzando la carretera por los tramos no vallados de modo que se ha decidido hacer pequeños túneles o «pasos de fauna». Se sabe que uno de estos túneles cubre tres tramos, es decir se estima que un lince no cruzará una carretera por la superficie si hay un paso subterráneo en el tramo en el que está o en alguno de los tramos adyacentes. Las preguntas que os hacíamos era cuál es el mínimo número de túneles que hay que hacer para evitar atropellos en diferentes configuraciones de carretera.
Este acertijo surge de uno de los problemas que se pusieron en los regionales de Madrid y Reus de ProgramaMe, y está publicado en ¡Acepta el reto!. Aunque nadie ha puesto su solución en los comentarios, ha habido varias personas que han resuelto el problema en la última semana, de modo que ¡enhorabuena a todos ellos! La próxima vez no seáis tan tímidos, y contarnos vuestra solución aquí 🙂
Vamos con la nuestra. La primera pregunta que os hacíamos era relativa a una carretera con la configuración .... que significa que tiene cuatro tramos, y ninguna valla. Dado que cada túnel cubre tres tramos, es imprescindible hacer dos túneles. Hay varias posiciones válidas para ellos (por ejemplo, si los marcamos con una t podríamos hacerlo t..t, t.t., .tt. o .t.t), pero es imposible evitar el cruce en todos los tramos con un único túnel.
La siguiente pregunta era ..X...X, donde una X representa una valla. En este caso necesitamos un túnel para el primer bloque sin vallas, y un segundo túnel para el segundo. Una configuración podría ser t.X.t.X. Observa que todos los tramos tienen o bien un túnel o valla, o un túnel adyacente.
La última pregunta era un poco más larga, X.XXX....X.X.X. Para cubrir el primer tramo sin valla necesitamos un túnel. La parte más interesante de esta pregunta es darse cuenta de que podemos poner túnel debajo de vallas lo que en este caso nos ahorrará túneles. En concreto, basta con 4 túneles; aunque hay varias formas de conseguirlo, una sería XtXXX.t..T.XtX donde T representa un tramo con túnel y valla.
Todas estas respuestas se pueden deducir con relativa facilidad gracias al sentido común, el problema es cómo programarlo 🙂 Para eso, basta con ir colocando túneles al ir recorriendo los tramos de carretera. En concreto, cuando nos planteamos qué hacer al llegar al tramo i asumiremos que todos los tramos anteriores están ya resueltos (y los linces no cruzarán la carretera por ellos). Si el tramo i tiene valla, entonces no hay nada de lo que preocuparse y pasamos al siguiente. Si no la tiene, entonces colocaremos un túnel en el tramo siguiente (es decir en i+1). Ese túnel cubrirá al tramo actual y a los dos siguientes, a si es que, independientemente de si esos dos tienen valla o no, nos los saltamos sin preocuparnos de ellos, y seguimos buscando. Fíjate que colocar el túnel en el tramo siguiente hace que se aproveche lo más posible. Si lo colocáramos en la posición i (la actual), el túnel estaría cubriendo también el tramo anterior, i-1, que, hemos dicho, estamos suponiendo que ya no será cruzado por ningún lince por nuestros túneles anteriores. Por tanto desaprovecharíamos un poco nuestro túnel recién puesto y la solución podría no ser la óptima.
Surge la pregunta de qué pasa al final de la carretera. Si tenemos una carretera XXX. en nuestra simulación colocaríamos un túnel más allá del final. En realidad la posición exacta de los túneles no nos la preguntan, sólo el número. Lo importante es que aquí necesitamos un único túnel, y eso es justo lo que nuestro algoritmo contestaría 🙂
Esta solución pertenece a la familia de los algoritmos voraces, que ya son viejos conocidos nuestros (sin ir más lejos, usamos uno en el acertijo anterior). En ellos, tomamos una decisión «local» (colocar o no un túnel) sin preocuparnos del problema completo, sólo de una pequeña parte (el tramo actual, no la configuración de toda la carretera). Además, tampoco nos replanteamos en ningún momento las decisiones tomadas por si resultaron no ser una buena idea. Aunque no siempre dan la solución óptima, en el caso del acertijo que nos ocupa sí lo hace, y de una manera muy sencilla de programar por lo que ¡nos lo quedamos!
Como siempre, si quieres programar tu solución y probarla, puedes hacerlo aquí.
¡Hasta el próximo!
Hola!
Vamos con el último acertijo antes de la final nacional de ProgramaMe. Esta vez está sacado de uno de los problemas de los regionales de Madrid y Reus. ¡Si alguno de los finalistas nos lee, así le damos la oportunidad de practicar!
El lince ibérico es una especie en peligro de extinción, por lo que se intenta que la actividad humana afecte a su hábitat lo menos posible. Sin embargo, una carretera cruza su territorio. Para evitar atropellos de linces, se pusieron vallas en algunos tramos que impedían que las cruzaran. Pero el resto de tramos siguen al descubierto y de vez en cuando aparece algún animal muerto por atropello.
Ahora se está planteando la posibilidad de hacer túneles por debajo de la carretera para que los linces crucen sin riesgo. Los ecologistas creen que un túnel en un tramo de carretera será usado por los linces que quieran cruzar en ese tramo y en los dos adyacentes. Así, por ejemplo, si tenemos una carretera con tres tramos sin valla, bastará con hacer un túnel en el tramo central para evitar más atropellos. Por su parte, en la siguiente carretera, donde ‘X‘ indica que ese tramo tiene una valla y ‘.‘ indica que no la tiene:
necesitaremos hacer dos túneles, uno en el segundo tramo y otro en el último. O en:
es suficiente hacer un túnel debajo de la última valla para evitar que los linces crucen por los dos tramos al descubierto.
¿Cuál es el mínimo número de túneles que hay que hacer para evitar atropellos en las siguientes carreteras?
- ....
- ..X...X
- X.XXX....X.X.X
¡Cuéntanos tus conclusiones en los comentarios! Y si crees que has encontrado una forma de programar tu solución y quieres probarla, puedes hacerlo aquí.
Hola!
Llega el momento de dar la solución a nuestro último acertijo. En él, os hablábamos de una población costera que ha colocado vallas publicitarias a lo largo del paseo marítimo, y de una empresa que quiere conseguir que los viandantes vean su anuncio al menos un número de veces en sus paseos. Para eso, conoce los puntos de inicio y de fin de los recorridos que realizan, y necesita averiguar el mínimo número de vallas que debe alquilar para conseguir su objetivo.
Gualterio nos dio su solución y… ¡acertó! Aunque haya sido en el tiempo de descuento por nuestro retraso en la publicación de la solución 🙂 su contribución es igual de válida de modo que ¡enhorabuena, un acertijo más! 🙂
Pero basta de preámbulos y vamos con la explicación. La primera situación por la que os preguntábamos era fácil. En ella, la empresa quiere que los turistas vean su anuncio al menos 5 veces, y hay sólo dos recorridos a cubrir:
- Del número 1 al número 10 o, abreviando, (1, 10).
- Del número 30 al 20: (30,20)
En este caso la respuesta es muy sencilla, dado que los dos recorridos no se solapan. Las vallas que la empresa alquile para que los turistas que hacen el camino (1,10) vean su anuncio no serán vistas por los turistas que hagan el recorrido (30, 20). Por tanto, será necesario alquilar 5 vallas para cada uno, por lo que el mínimo será de 10.
La siguiente pregunta es un poco más complicada. Consistía también en conseguir que los turistas vieran 5 vallas publicitarias, pero ahora los recorridos son (17-21), (10-20), (25-5), donde sí hay solapamiento.
| 17-21 | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10-20 | |||||||||||||||||||||||||
| 25-5 |
Con la imagen delante, no resulta ya tan complicado. Lo que queremos es minimizar el número de vallas que alquilamos, de modo que queremos coger aquellas que más turistas vean. Claramente en este caso tenemos que coger las cinco vallas del rango 17-21. Las 5 serán vistas por los turistas del último recorrido, (25, 5) de modo que para ellos no hay que alquilar más. Tan sólo nos falta una más para el rango 10-20. Podemos coger la que queramos (por ejemplo la situada en el número 16):
| 17-21 | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10-20 | |||||||||||||||||||||||||
| 25-5 | |||||||||||||||||||||||||
| Alq. |
Alquilando las vallas marcadas en la última fila, se puede comprobar que todos los turistas ven al menos 5 veces nuestro anuncio.
¿Cómo podemos hacer el cálculo de una manera sistemática? Si el número de recorridos crece, cada vez resultará más complicado utilizar la intuición para colocar las vallas, incluso aunque nos hagamos el dibujo. De hecho, la última pregunta es bastante más larga: 6 vallas y recorridos (7, 10), (25, 33), (32, 62), (50, 20), (44, 9), (50, 86) y (24, 19).
Para resolverlo, lo que hacemos es utilizar un algoritmo voraz diseñado para la ocasión, tal y como ya hicimos en otros acertijos anteriores. Lo que haremos será ir alquilando vallas para conseguir que cada recorrido de un turista tenga nuestros 6 anuncios, de tal manera que garanticemos que, al final, el número de vallas alquiladas sea el mínimo necesario.
¿Y cómo lo conseguimos? La idea principal es ordenar los recorridos por punto de finalización. Da igual lo largo o cortos que sean. Lo importante es dónde acaban. Ten en cuenta que como el orden es importante, usaremos siempre el sentido «de menor a mayor» en los recorridos de manera que, por ejemplo, al recorrido (50, 20) le daremos la vuelta para simular que todos los turistas van en sentido ascendente de la numeración. Esto no es importante para el resultado final, pero sí para que nuestro mecanismo de obtención de la respuesta funcione.
Con esta idea, los recorridos que tenemos que cubrir (ordenados ya de menor a mayor por punto de finalización) son (7, 10), (19, 24), (25, 33), (9, 44), (20, 50), (32, 62), (50, 86). Fijate que, por ejemplo, el recorrido (9, 44) empieza antes que el (25,33). Pero lo analizaremos después porque acaba más tarde.
Ahora empezamos a analizar cada recorrido con el primero, (7, 10). Tenemos que conseguir que los turistas vean 6 vallas, y sin embargo estos turistas sólo recorren 4. Tendremos que alquilarlas todas y conformarnos con eso. Para los turistas (19, 24) nos toca hacer lo mismo: alquilar las 6 vallas de su recorrido.
El acertijo se pone más interesante con el siguiente, (25, 33). Tenemos que alquilar 6 vallas; pero, ¿cuales? Dado que tenemos ordenados los recorridos por finalización nos interesa comprar las vallas del final para que así los siguientes recorridos, que siempre acaban más tarde, tengan posibilidad de ver también las vallas que alquilamos ahora. Es decir, sin saber de antemano qué vendrá después, es mejor alquilar las vallas (28, 33), en lugar de alquilar (25, 30), porque todos los recorridos que vendrán después terminan pasado el número 33, y por tanto hay más probabilidades que vean la valla en la posición 28 que la valla en la posición 25 (dependiendo de dónde empiecen).
Tras haber analizado los tres primeros recorridos, por tanto, hemos alquilado las vallas (7, 10), (19, 24) y (28, 33). El siguiente recorrido que procesamos es (9, 44) pero este recorrido ya tiene dentro más de 6 de nuestros anuncios gracias a las vallas alquiladas antes, por lo que no añadimos ninguna más. Con (20, 50) ocurre igual.
Con el penúltimo recorrido, (32, 62), ocurre algo intermedio. En él son visibles dos vallas ya alquiladas, la 32 y la 33. Quedan 4 más por alquilar. Pero… ¿cuales? Como hemos dicho antes, lo más conservador es alquilarlas al final, en el rango (59, 62). De esa manera los recorridos que vengan después (y que acaban más tarde) podrían aprovecharse de ellas. Y… ¡así es! El último recorrido, (50, 86) ve esas 4 vallas también. Si hubiéramos alquilado vallas por detrás del 50 no las habríamos reutilizado.
Sólo falta alquilar dos vallas más para el último recorrido (en 85 y 86) y habremos terminado. Al final hemos alquilado (7, 10), (19, 24), (28, 33), (59, 62) y (85, 86), que hacen un total de 22 vallas. Podemos conseguir que los turistas vean nuestras 6 vallas alquilando otras, pero nunca podremos conseguirlo con menos de 22 vallas 🙂
Ahora que os hemos contado el truco del acertijo, quizá queráis intentar programarlo. Si lo hacéis y queréis probar vuestra solución, podéis hacerlo aquí.
¡Hasta el próximo!
Hola!
Andamos un poco liados con los preparativos para ProgramaMe, y no hacemos más que acumular retrasos con los acertijos 😦 Para que no paséis toda esta semana sin algo en que entreteneros :-p, y aunque sea un día extraño, vamos a proponeros hoy un acertijo. Pero para dar tiempo a que lo penséis, os contaremos nuestra solución al final de la semana que viene, en lugar de este domingo.
En un intento de recaudar dinero, el ayuntamiento de un pueblo costero ha decidido poblar todo el paseo marítimo de vallas publicitarias, para desesperación de los vecinos. Ha colocado una delante de cada portal, que están numerados consecutivamente (no sólo usando los números pares o impares) al haber únicamente casas en un lado.
Una empresa local ha decidido que, para aprovechar la afluencia de turistas durante el verano, va a contratar algunas de esas vallas para hacer una campaña agresiva de publicidad. En concreto, ha analizado los «puntos calientes» del paseo marítimo (como hoteles y grandes edificios residenciales por un lado, y heladerías o chiringuitos por otro) para tener los puntos de origen y destino de los turistas. Tienen así un conjunto de recorridos habituales de sus potenciales clientes.
Ahora quieren conseguir que todos los turistas vean su anuncio un número mínimo de veces (para convencerles por aburrimiento). Pero no quieren gastarse demasiado dinero en contratar vallas publicitarias, a si es que quieren conseguirlo con el menor presupuesto posible. Por ejemplo, imaginemos que sabemos que los turistas hacen tres posibles recorridos:
- Del número 1 al 15. Por abreviar, (1, 15)
- (13, 30)
- (27, 45)
La empresa quiere conseguir que todos vean el anuncio al menos 7 veces; en estas condiciones el mínimo número de vallas que hay que contratar es de 14, siempre que se escojan con inteligencia.
¿Cuál sería ese mínimo en las siguientes situaciones?
- 5 vallas y recorridos (1, 10) y (30, 20).
- 5 vallas y recorridos (17-21), (10-20), (25-5)
- 6 vallas y recorridos (7, 10), (25, 33), (32, 62), (50, 20), (44, 9), (50, 86) y (24, 19)
El último es bastante más largo que los otros dos… la idea es que los dos primeros sirvan para encontrar un modo sistemático de dar con la respuesta, y el último se use para probarlo 🙂
Ten en cuenta que los turistas se desplazan en los dos sentidos por el paseo marítimo, de ahí que en algunos casos vayan en sentido decreciente de la numeración. Además, algunos recorridos son demasiado cortos como para conseguir ver el mínimo número de vallas. En ese caso, la empresa anunciante se conforma con que vean sólo anuncios suyos y no de otras empresas.
Si das con las respuestas… ¡cuéntalas en los comentarios! Y, como siempre, si programas la solución y quieres probarla, puedes hacerlo aquí.
¡Hasta la semana que viene!
¡Hola!
Llega el momento de dar la solución a nuestro acertijo de la semana. En él os preguntábamos cuántos números de 6 bits tienen exactamente 3 bits a 1, y cuántos de 8 tienen 5. Gualterio nos dió sus respuestas: 20 y 56 respectivamente. Y no sólo acertó, sino que se atrevió a dar respuesta a una pregunta más, la cantidad de números de 20 bits con 7 bits a 1. ¡Siempre que da su respuesta nos hace a nosotros otra pregunta! 🙂 Efectivamente, en ese caso 77.520 números diferentes con exactamente 7 bits a 1. Pero, ¿cómo se resuelve sin tener que escribir todas las configuraciones?
Vamos a contaros dos posibles formas de afrontar el problema. El primero es el modo «matemático» que es cómodo para ser resuelto a mano; el segundo es el «de programador» que permite solucionar el acertijo sin necesidad de saberse las matemáticas que hay por debajo. Como siempre, nos gusta que nuestros acertijos puedan ser resueltos a mano, de forma que empezaremos con el primero.
La pregunta entra dentro del campo de las matemáticas conocida como combinatoria, que estudia la «enumeración de configuraciones que satisfacen ciertas condiciones establecidas». Da respuestas a preguntas como «¿cuántas posibles quinielas se pueden hacer?» o «¿de cuántas formas se pueden sentar un grupo de personas alrededor de una mesa?».
En el caso que nos ocupa, la pregunta es la cantidad de números de 6 bits que tienen exactamente 3 bits a 1. Podemos ver este problema como que tenemos «6 objetos» (el bit a 1 en la primera posición del número, el bit a 1 en la segunda posición del número, etcétera), y queremos saber el número de formas de coger 3 de esos objetos, sin importar el orden. Es decir, la opción de decir «voy a poner a 1 el bit 2, el 4 y el 5» es la misma que la opción «voy a poner a 1 el bit 5, el 4 y el 2», porque el resultado será el mismo. Dicho de otro modo, ¿de cuántas formas posibles podemos escoger 3 objetos de un total de 6, sin importar el orden?
A esto los matemáticos lo conocen como combinaciones y se escribe como . La fórmula general para calcular el valor es:
Una vez que sabemos esto, es fácil averiguar las respuestas a las preguntas:
Pero… ¡ten cuidado! Aunque este mecanismo es suficiente para resolver nuestras preguntas, si intentas usarlo para resolver el problema original en ¡Acepta el reto! tendrás problemas. Los factoriales crecen muy deprisa y tendrás desbordamientos. Y hacer el módulo 1.000.000.007 que pide el ejercicio no es tan fácil a la hora de dividir, y te tocará buscar los inversos en ese módulo… y eso ¡se complica! De modo que aunque las matemáticas nos han venido bien para resolver el acertijo a mano, para usarlas en la solución programada tendríamos que complicarlas un poco más y es preferible ver la solución para programadores…
En concreto, revisemos la pregunta. ¿Cuántos números hay de 6 bits con 3 bits a 1? Podemos resolverlo recursivamente (con una recurrencia) si en cada paso establecemos el valor de un bit y dejamos la responsabilidad del resto en la llamada recurvisa. En concreto, la respuesta a nuestra pregunta es:
- La cantidad de números de 5 bits que tengan 3 bits a uno (en el bit actual hemos escrito un 0), más
- La cantidad de números de 5 bits que tengan 2 bits a uno (en el bit actual hemos escrito un 1).
Programar esto no es difícil; falta añadir los casos base y el módulo 1.000.000.007 que nos pide el problema en Acepta el reto. La única pega es que es muy lento (por la recursión doble) de modo que lo mejor es guardarlo en una tabla y… ¡lo tendréis resuelto!
Intentadlo, que no es muy difícil, enviad vuestra solución aquí y nos contáis cómo os fue.
¡Hasta el próximo!
¡Hola!
¡Caracoles! La semana pasada nos pilló el toro y se pasó en blanco sin acertijo 😦 Sentimos haberos hecho esperar… pero ¡ya estamos aquí! Hemos vuelto para haceros pensar un rato 🙂
Ya os hemos hablado antes de los números binarios. Los hemos usado en torneos de tenis, máquinas de monedas e incluso entrelazados con los números de Fibonacci. Como podéis ver… dan mucho juego… ¡y lo que te rondaré, morena! 🙂 Para demostrarlo… vamos con otra pregunta sobre ellos 😉
Si escribimos, por ejemplo, todos los números de 3 bits obtendremos:
000
001
010
011
100
101
110
111
Podéis ver que entre las 8 opciones disponibles hay 3 que tienen un bit a 1, otras 3 que tienen 2, y 1 que tiene 3.
La pregunta es sencilla: ¿cuántos números de 6 bits tienen exactamente 3 bits a 1? ¿Y cuántos de 8 bits tienen 5?
Si das con la solución… ¡cuéntanosla! Y, como siempre, si eres capaz de programarla, puedes probar tu código aquí. Pero… ¡cuidado! El problema en ‘¡Acepta el reto!’ esconde una sorpresa por los tamaños…
¡Venga que no es difícil!
¡Hola!
Se termina la semana y vuestro tiempo para darnos la solución al acertijo que os proponíamos el lunes pasado. En él, os preguntábamos cuál es el máximo número de regiones interiores que se pueden formar en una elipse si colocamos sobre su contorno un determinado número de puntos y pintamos líneas uniendo todos con todos. Como ejemplo, os decíamos que con 2 puntos se formaban 2 regiones, con 3 puntos se formaban 4, y con 4 puntos se formaban 8 regiones.
Concretamente, os preguntábamos cuántas regiones interiores se formaban poniendo 6 y 10 puntos diferentes. Si estáis habituados a los números binarios rápidamente os habréis percatado de que las soluciones de los ejemplos son las potencias de dos: 21, 22 y 23. La intuición podría en ese caso llevaros a pensar que con 6 puntos se formarían 25 regiones (32) y con 10 se formarían 29 (512). Pero… ¡os equivocaríais! De hecho, este acertijo (que se conoce como «el problema del círculo de Moser») se suele utilizar como una prueba de que sacar conclusiones precipitadas utilizando sólo unos cuántos valores iniciales de una secuencia puede llevar a respuestas incorrectas 🙂
Pero nuestro lector Gualterio, que se está convirtiendo en un asiduo 🙂 no cayó en la trampa. Su respuesta, una vez más, ¡fue la correcta! Efectivamente, con 6 puntos se forman 31 regiones internas, y con 10 se forman 256. Como os decíamos el lunes, llegar a estas soluciones es cuestión de calma y tenacidad (especialmente la de 10 puntos). Pero la pregunta que Gualterio se contestó a sí mismo de una elipse con 100 millones de puntos y un total de 4.166.666.416.666.676.249.999.925.000.001 regiones está fuera del alcance del tiempo de una vida humana, de modo que claramente hay una solución mejor 🙂
La que os contaremos aquí necesitará hacer bastantes cuentas (repetitivas), por lo que, como os contábamos el lunes, es mejor resolverlo con un ordenador. Hay también una solución que puede utilizarse para calcular el resultado de una manera mucho más rápida que podría usarse incluso con una calculadora en unos segundos, pero llegar a ella es más complicado, a si es que, por una vez, nos conformaremos con la solución para programadores 🙂
Vamos allá. Lo primero de lo que hay que darse cuenta es de que cuando pintamos una nueva arista uniendo dos puntos, partimos en dos aquellas regiones por las que pasamos. Por ejemplo, si tenemos dos puntos, la figura que formaremos será similar a la siguiente:
Si pensáis que al principio había una única región (ocupando el interior completo de la elipse), al dibujar la linea la región queda dividida en dos partes (no necesariamente iguales, claro). Dicho de otro otro modo, de una región inicial, hemos sacado dos, y por tanto el número de regiones totales se ha incrementado en uno.
Con tres puntos, la situación es similar a la siguiente:
Al añadir el tercer punto, hay que pintar dos aristas nuevas, cada una de las cuales divide en dos la única región que atraviesa. Por tanto, cada una incrementa en uno el número de regiones totales, y pasamos de 2 a 4 regiones.
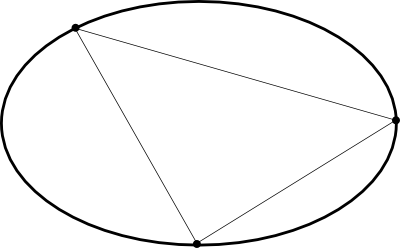
Con cuatro puntos el asunto se pone más emocionante:
Fijaos en la linea que va del punto superior izquierdo al inferior derecho. Esa linea atraviesa dos regiones pues cruza una arista previa ya existente. Por tanto, significa que divide dos regiones anteriores pasando a formar cuatro más pequeñas. Por tanto, la arista incrementa en dos el número de regiones finales.
La conclusión que hay que sacar de este análisis es que cada nueva linea añade tantas regiones como lineas anteriores atraviese más una. Si lo pensáis un poco no os resultará difícil convenceros.
Por tanto, lo que necesitamos saber es ¿cuál es el número máximo de lineas que cruzarán las lineas nuevas? Para eso, vamos a añadir un quinto punto a la figura anterior, y pintaremos una única diagonal:
El nuevo punto es el etiquetado como 5, y hemos puesto una única arista, que lo une con el punto 3. Como podéis ver, cruza dos aristas previas (en los puntos a y b). ¿Por qué se corta en dos? Se corta en dos porque la nueva arista deja a un lado un punto, y al otro dos. Como todos los vértices están unidos con todos los demás, eso significa que hay 1×2 (=2) aristas que pasan de un lado hacia el otro, y por tanto, 2 cruces. Eso significa que esa arista genera 3 nuevas regiones internas.
Si en lugar de dibujar la arista uniendo el punto 5 con el 3 hubiéramos pintado la arista uniendo el 5 con el 4, en un lado no habría quedado ningún vértice, y al otro lado habrían quedado 3; 0×3 es 0, por lo que no hay corte de aristas y por tanto la arista 5-4 sólo crea una región nueva, al igual que, podéis comprobarlo, ocurre con la arista 5-1. Por su parte, la arista 5-2 cruza otras dos (como la 5-3), por lo que crea tres regiones más.
Una vez que nos hemos dado cuenta de esto, no es demasiado difícil generalizar. Por ejemplo, si tuviéramos ya colocados 7 puntos y estuviéramos colocando el octavo, tendríamos:
- Dos diagonales que dejan 0 vértices a un lado y 6 a otro, por lo que ninguna se corta con nada y generan una única región (cada una).
- Dos diagonales que dejan 1 vértice a un lado y 5 a otro, por lo que se cortan con 1×5 diagonales, y añaden 6 regiones cada una.
- Dos diagonales que dejan 2 vértices a un lado y 4 a otro, por lo que se cortan con 2×4 diagonales y añaden 8 regiones cada una.
- Una diagonal que deja 3 vértices a un lado y otros tres a otro, lo que genera 3×3 + 1 regiones nuevas.
¿Veis el patrón? Los que programéis, seguro que seréis capaces de hacer un bucle para realizar este cálculo. Además, esto hay que repetirlo para cada punto nuevo añadido (desde 1 hasta 6 o hasta 10 en nuestras dos preguntas), de modo que se necesitan dos bucles anidados. Si lo hacéis con un poco de cuidado, llegaréis a la solución dada por Gualterio 🙂
Aquellos lectores inclinados hacia las matemáticas (que alguno hay 🙂 ) en lugar de (o, quizá, «además de») bucles también verán sumatorios. En ese caso, no es demasiado difícil (aunque sí un poco laborioso) escribir y desarrollar los sumatorios para llegar a un polinomio con el que calcular el resultado directamente, sin necesidad de un ordenador que nos ahorre el trabajo tedioso de iterar.
Y… para los matemáticos de verdad… este problema puede resolverse en realidad aprovechándose del invariante topológico de Euler (χ) que relaciona el número de aristas, vértices y caras de poliedros. Para eso, hay que considerar a la figura que estamos construyendo como un grafo planar por lo que su invariante topológico es 2. Usando combinatoria, se puede sacar el número de aristas y de vértices (interiores) que se forman a partir de los n vértices exteriores, y usar la χ de Euler para averiguar el número de caras (regiones interiores).
Pero… a los humanos normales nos sirve la solución de bucles 🙂 Si la programáis, recordad que podéis probar vuestra solución aquí (aunque necesitaréis utilizar enteros de precisión arbitraria).
¡Hasta el próximo!
¡Hola!
Esta vez os proponemos un acertijo de geometría. Si dibujamos una elipse y elegimos dos puntos cualesquiera en su contorno, al unir esos dos puntos la elipse queda dividida en dos partes:
Si ponemos tres, crearemos 4 partes:
El asunto se pone interesante con cuatro puntos. Al unir todos con todos, el número de secciones de la elipse crece considerablemente, y pasamos a tener 8:
¿En cuántas partes queda dividida como máximo una elipse si elegimos 6 puntos diferentes en su contorno y los unimos todos entre sí? ¿Y si elegimos 10?
Para resolver este acertijo, dependiendo de vuestros conocimientos e inquietudes, tendréis tres opciones:
- Contestar a las dos preguntas usando lápiz y papel y dedicándole un rato a pintar.
- Pensar un poco (ayudados de lápiz y papel) y llegar a una forma de programar el cálculo para ahorraros un proceso repetitivo y aburrido.
- Pensar «un mucho» 🙂 y llegar a una forma de calcular el número con unas cuantas operaciones matemáticas.
Ya sabéis que solemos poner acertijos de este tipo, y nos gusta luego resolverlos con la última opción, de modo que cualquiera (incluso los no programadores) puedan contestar a nuestras preguntas rápidamente. Sin embargo, en esta ocasión, seremos infieles a nuestros propios principios, y nos quedaremos con la segunda opción. Por eso, las preguntas que os hemos hecho son intencionadamente «pequeñas», para que los no programadores puedan contestarlas manualmente pintando. De otro modo, habríamos sido un poco más brutos, preguntándoos por 50 o por 100 puntos 🙂
Eso sí, como siempre, si encontráis la forma de programarlo, podéis probar vuestras soluciones aquí. Y ¡¡no olvidéis contárnoslo en los comentarios!